PELUANG
- Kaidah Pencacahan, Permutasi dan Kombinasi
- Kaidah Pencacahan
Apabila peristiwa pertama dapat terjadi dalam p cara berbeda, peristiwa kedua q cara berbeda, peristiwa ketiga r cara berbeda, dan seterusnya, maka banyaknya cara yang berbeda terhadap rangkaian berurutan seperti itu adalah = p x q r x ..
- Faktorial
Perkalian n bilangan asli pertama disebut n faktorial, dinotasikan dengan n!
n! = 1 x 2 x 3 x 4 x …. x (n – 1) x n
atau n! = n x (n – 1) x (n – 2) x ….. x 4 x 3 x 2 x 1
- Permutasi
Cara menempatkan n buah unsur ke dalam r tempat yang tersedia dengan urutan diperhatikan disebut permutasi r unsur dari n unsur(r ≤ n) yang dinotasikan dengan nPr atau P(n,r) atau 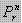 atau Pn,r
atau Pn,r
- Banyaknya permutasi n unsur berbeda disusun n unsur(seluruhnya) adalah : P = n!
- Banyaknya Permutasi yang dapat disusun dari n anggota suatu himpunan diambil r unsur anggota pada satu saat adalah :
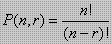
- Banyaknya permutasi jika ada beberapa elemen/unsur yang sama adalah :
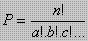
- Banyaknya permutasi siklis adalah permutasi yang disusun secara melingkar dengan memperhatikan urutannya(arah putarannya) adalah :
P = (n – 1)!
- Kombinasi
Cara menempatkan n buah unsur ke dalam r tempat yang tersedia dengan urutan tidak diperhatikan
disebut Kombinasi r unsur dari n unsur(r ≤ n) yang dinotasikan dengan nCr atau C(n,r) atau 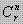 atau Cn,r
atau Cn,r
Kombinasi n unsur berbeda disusun r unsur dirumuskan :
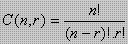
- Binomial Newton
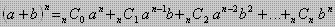
- Peluang Suatu Kejadian
- Dalam suatu percobaan :
- Semua hasil yang mungkin disebut ruang sampel
- Setiap anggota dalam ruang sampel disebut titik sampel
- Hasil yang diharapkan disebut kejadian
- Definisi Peluang
Peluang kejadian A dinotasikan dengan P(A) adalah perbandingan banyaknya hasil kejadian A dinotasikan n(A)
terhadap banyaknya semua hasil yang mungkin dinotasikan dengan n(S) dalam suatu percobaan.
Kisaran nilai peluang suatu kejadian A adalah 0 ≤ P(A) ≤ 1.
Jika P(A) = 0 disebut kemustahilan dan P(A) = 1 disebut kepastian
- Frekuensi Harapan
Frekuensi Harapan kejadian A adalah banyaknya kejadian A yang diharapkan dalam beberapa kali percobaan
Jika percobaan dilakukan sebanyak n kali maka frekuensi harapan kejadian A dirumuskan : Fh(A) = n x P(A)
- Peluang Komplemen Suatu Kejadian
Jika Ac kejadian selain A, maka P(A)c = 1 – P(A) atau
P(A)c + P(A) = 1
P(A)c = peluang komplemen kejadian A atau peluang kejadian selain kejadian A
- Kejadian Majemuk
- Untuk sembarang kejadian A atau B berlaku :
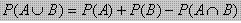
- Peluang dua Kejadian saling lepas(asing)
Jika 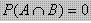 maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
Besarnya peluang dua kejadian saling lepas(asing) adalah : 
- Peluang dua kejadian saling bebas
Bila kejadian A tidak mempengaruhi terjadinya B dan sebaliknya, maka kejadian semacam ini disebut dua kejadian saling bebas
Peluang dua kejadian saling bebas dirumuskan : 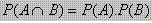
- Peluang dua kejadian tak bebas(bersyarat/bergantungan)
Apabila kejadian kedua(B) adalah kejadian setelah terjadinya kejadian pertama A, dinotasikan (B/A),
maka dua kejadian tersebut merupakan dua kejadian tak bebas(bersyarat)
Peluang dua kejadian tak bebas dirumuskan : 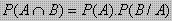
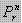 atau Pn,r
atau Pn,r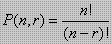
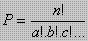
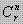 atau Cn,r
atau Cn,r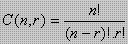
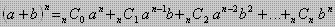
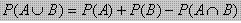
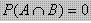 maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
maka dua kejadian tersebut merupakan dua kejadian saling lepas artinya bila terjadi A tidak mungkin terjadi B.
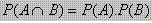
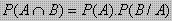
 Categories :
Categories :  23.48
23.48
 science
science


0 komentar:
Posting Komentar